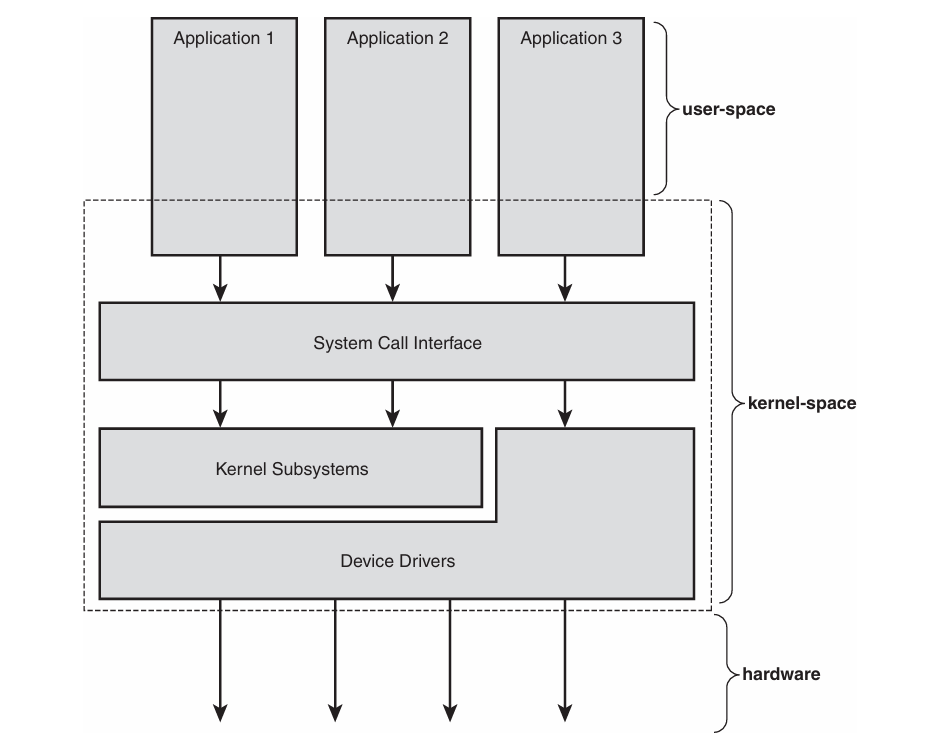
操作系统基础 | 2.6 linux组成概述2
程序(Programs)
- 程序通常有两种形式:
- 源代码:人类可读的文本,使用如 C
这样的编程语言编写。
- 二进制机器码:计算机可执行的指令。源代码需经过编译和链接,才能变为机器码。
- 源代码:人类可读的文本,使用如 C
这样的编程语言编写。
- 脚本(script)是包含命令的文本文件,由 shell 或其他命令解释器直接处理。
- “程序”这两个含义通常可以互换,因为编译和链接会将源代码转换为等价的二进制代码。
过滤器(Filters)
- 过滤器是指一类程序:从标准输入(stdin)读取数据,处理后将结果写到标准输出(stdout)。
- 常见过滤器有:
cat、grep、tr、sort、wc、sed、awk等。
命令行参数(Command-line arguments)
- 在 C 语言中,程序可以通过 main 函数的参数访问命令行参数:
1
int main(int argc, char *argv[])
argc:参数个数argv:参数字符串数组,argv[0]通常是程序名
进程(Processes)
- 进程是正在运行的程序实例。
- 当程序被执行时,内核会将其代码加载到虚拟内存,分配变量空间,并建立记录进程信息的数据结构(如进程ID、终止状态、用户ID、组ID等)。
- 内核负责在进程间分配和管理有限资源(如内存、CPU、网络带宽等),进程结束时,资源会被回收。
进程内存布局
进程的内存逻辑上分为以下几个部分(段): - Text:程序指令(代码段) - Data:静态变量 - Heap:动态分配内存区域 - Stack:函数调用和局部变量的栈空间
进程创建与程序执行
- 进程可通过
fork()系统调用创建新进程。调用fork()的为父进程,新创建的为子进程。 - 子进程会复制父进程的数据、堆和栈(代码段通常只读并共享)。
- 子进程可以继续执行父进程的代码,也可以通过
execve()系统调用加载并执行新程序。execve()会用新程序的代码和数据替换原有的段。 - C 标准库还提供了一系列以
exec开头的函数,都是对execve()的封装,统称为exec()。
进程ID与父进程ID
- 每个进程有唯一的进程ID(PID)。
- 每个进程还有一个父进程ID(PPID),表示哪个进程创建了它。
进程终止与终止状态
- 进程可以通过
_exit()系统调用(或相关的exit()库函数)主动终止,也可以被信号杀死。 - 进程终止时会返回一个终止状态(小的非负整数),父进程可以通过
wait()系统调用获取。 - 约定:终止状态为 0 表示成功,非零表示出错。大多数 shell 用变量
$?保存上一个程序的终止状态。 整理与翻译如下:
进程的用户和组标识(凭证)
每个进程都关联有多个用户ID(UID)和组ID(GID),包括:
- 实际用户ID(real UID)和实际组ID(real GID):标识进程所属的用户和组。新进程从父进程继承这些ID。登录 shell 的实际UID和GID来自系统密码文件(/etc/passwd)中的相应字段。
- 有效用户ID(effective UID)和有效组ID(effective GID):这两个ID(加上补充组ID)用于判断进程访问受保护资源(如文件、进程间通信对象)时的权限。通常有效ID与实际ID相同。更改有效ID可以让进程临时获得其他用户或组的权限。
- 补充组ID(supplementary group IDs):标识进程所属的其他组。新进程从父进程继承这些ID,登录 shell 的补充组ID来自系统组文件(/etc/group)。
特权进程
- 在传统 UNIX 系统中,有效用户ID为0(即超级用户 root)的进程被称为特权进程,可以绕过内核的权限检查。
- 其他用户运行的进程称为非特权进程,其有效用户ID非0,必须遵守内核的权限规则。
- 进程可以通过由特权进程创建(如 root 启动的 shell),或通过 set-user-ID 机制(程序文件设置了 setuid 位,进程获得该文件所有者的有效UID)获得特权。
能力(Capabilities)
- 从 Linux 2.2 内核开始,传统上属于超级用户的权限被细分为多个能力(capabilities)。
- 每个特权操作都对应一个能力,进程只有拥有相应能力才能执行该操作。
- 传统的超级用户进程(有效UID为0)等价于拥有所有能力的进程。
- 只授予进程部分能力,可以让它执行部分特权操作,同时限制其他操作。
- 能力名称以
CAP_开头,如CAP_KILL。
init 进程
- 系统启动时,内核会创建一个特殊进程
init(所有进程的“父进程”),其程序文件为
/sbin/init。 - 系统中所有进程都是由 init 或其子孙进程通过 fork() 创建的。
- init 进程的进程ID永远为1,拥有超级用户权限,不能被杀死(即使是超级用户也不行),只会在系统关机时终止。
- init 的主要任务是创建和管理系统运行所需的各种进程。
守护进程(Daemon processes)
- 守护进程是一类特殊用途的进程,由系统创建和管理,其特点包括:
- 生命周期长:通常在系统启动时启动,直到系统关闭才结束。
- 后台运行:没有控制终端,无法直接读取输入或输出到终端。
- 常见的守护进程有
syslogd(记录系统日志)、httpd(提供网页服务)等。
环境变量列表(Environment list)
- 每个进程都有一个环境变量列表,存储在进程的用户空间内存中。每个环境变量由名称和值组成。
- 通过
fork()创建新进程时,子进程会继承父进程的环境变量列表。这为父进程向子进程传递信息提供了机制。 - 进程用
exec()执行新程序时,可以选择继承原有环境变量,或指定新的环境变量。 - 在大多数 shell 中,用
export命令(C shell 用setenv)创建环境变量,例如:1
export MYVAR='Hello world'
- C 程序可以通过外部变量
char **environ访问环境变量,也可用相关库函数获取和修改环境变量。 - 环境变量用途广泛,如
HOME(用户主目录)、PATH(shell 查找命令的目录列表)等。
资源限制(Resource limits)
- 每个进程都会消耗资源,如打开的文件数、内存、CPU 时间等。
- 进程可用
setrlimit()系统调用设置资源消耗的上限。每种资源限制有两个值:- 软限制(soft limit):进程实际可用的资源上限。
- 硬限制(hard limit):软限制可调整的最大值。
- 非特权进程可以将软限制调整到硬限制以内的任意值,但只能降低硬限制,不能提高。
- 新进程通过
fork()创建时,会继承父进程的资源限制设置。 - shell 可用
ulimit命令(C shell 用limit)调整资源限制,这些设置会被子进程继承。