513. 找树左下角的值
迭代法
此题用迭代法做比较简单，掌握层序遍历即可
⚠️
注意不可直接写：for (int i = 0; i < layer.size(); i++)
layer.size()
在循环过程中是动态变化的，因为在循环中同时
pop() 和 push()，这会让 size()
的结果发生变化。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> layer;
layer.push(root);
int val;
while(!layer.empty()){
int sz = layer.size();
for(int i = 0 ; i< sz;i++){
TreeNode* cur = layer.front();
layer.pop();
if(cur->left)layer.push(cur->left);
if(cur->right)layer.push(cur->right);
if(i == 0)val = cur->val;
}
}
return val;
}
};
|
递归法
全局找值用全局变量即可，先从左子树开始递归，返回的就是左边节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public:
int maxDepth = 0;
int leftVal = INT_MIN;
void findVal(TreeNode* root, int depth){
if(root)depth++;
if(depth > maxDepth){
leftVal = root->val;
maxDepth = depth;
}
if(root->left){
findVal(root->left, depth);
}
if(root->right){
findVal(root->right, depth);
}
}
int findBottomLeftValue(TreeNode* root) {
findVal(root, 0);
return leftVal;
}
};
|
112. 路径总和
1
2
3
4
5
6
7
8
9
10
| class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root)return false;
if((!root->left && !root->right) && (root->val == targetSum))return true;
bool hasLeft = hasPathSum(root->left, targetSum - root->val);
bool hasRight = hasPathSum(root->right, targetSum - root->val);
return hasLeft || hasRight;
}
};
|
113. 路径总和ii
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
vector<vector<int>> result;
void pathSum(TreeNode* root, int target, vector<int> path){
path.push_back(root->val);
if((!root->left && !root->right) && root->val == target){
result.push_back(path);
}
if(root->left)pathSum(root->left, target - root->val, path);
if(root->right)pathSum(root->right, target - root->val, path);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if(!root)return result;
vector<int> path;
pathSum(root, targetSum, path);
return result;
}
};
|
106.从中序与后序遍历序列构造二叉树
有几种方法可以取出vector的一部分：
✅ 用迭代器构造
vector（构造函数）
1
| std::vector<int> v2(v1.begin(), v1.begin() + 3);
|
- 创建一个新的 vector
- 是构造函数，用于初始化
- 执行的是复制构造过程
✅ assign 方法
1
| v2.assign(v1.begin(), v1.begin() + 3);
|
- 修改已有的 vector 内容
- 是成员函数，不是构造
- 会清除原内容，然后从指定范围赋值
✅ std::span
1
2
3
| std::vector<int> original = {10, 20, 30, 40, 50, 60};
std::span<int> subspan(original.data() + 2, 3);
|
std::span 仅在 C++20 及以上版本中可用- 本身不支持负索引，但可以通过手动计算偏移量
不重复定义vector，每次用下标索引来分割性能会更好 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.empty())return nullptr;
if(inorder.size() == 1){
TreeNode* rt = new TreeNode(inorder[0]);
return rt;
}
int rootVal = postorder[postorder.size()-1];
TreeNode* root = new TreeNode(rootVal);
for(int i=0;i<inorder.size();i++){
if(inorder[i] == rootVal){
if(i>0){
vector<int> leftIn(inorder.begin(), inorder.begin()+i);
vector<int> leftPost(postorder.begin(), postorder.begin()+i);
root->left = buildTree(leftIn, leftPost);
}
if(i<(inorder.size()-1)){
vector<int> rightIn(inorder.begin()+i+1, inorder.end());
vector<int> rightPost(postorder.begin()+i, postorder.end()-1);
root->right = buildTree(rightIn, rightPost);
}
break;
}
}
return root;
}
};
|
105.从前序与中序遍历序列构造二叉树
尝试了一下，发现span的性能也就那样，并不理想。以后可以试试构造map和传区间下标的方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<span>
using namespace std;
class Solution {
public:
TreeNode* buildT(span<int> preorder, span<int> inorder){
TreeNode* root = new TreeNode(preorder[0]);
for(int i = 0; i<inorder.size();i++){
if(preorder[0] == inorder[i]){
if(i > 0){
span<int> left_p(preorder.data()+1,preorder.data()+i+1);
span<int> left_i(inorder.data(), inorder.data()+i);
root->left = buildT(left_p, left_i);
}
int right_l = inorder.size() - 1 - i;
if(right_l>0){
span<int> right_p(preorder.data()+i+1, preorder.data()+preorder.size());
span<int> right_i(inorder.data()+i+1, inorder.data()+inorder.size());
root->right = buildT(right_p, right_i);
}
}
}
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
span<int> pre(preorder.data(), preorder.data()+preorder.size());
span<int> in(inorder.data(), inorder.data()+inorder.size());
TreeNode* root = buildT(pre, in);
return root;
}
};
|
*
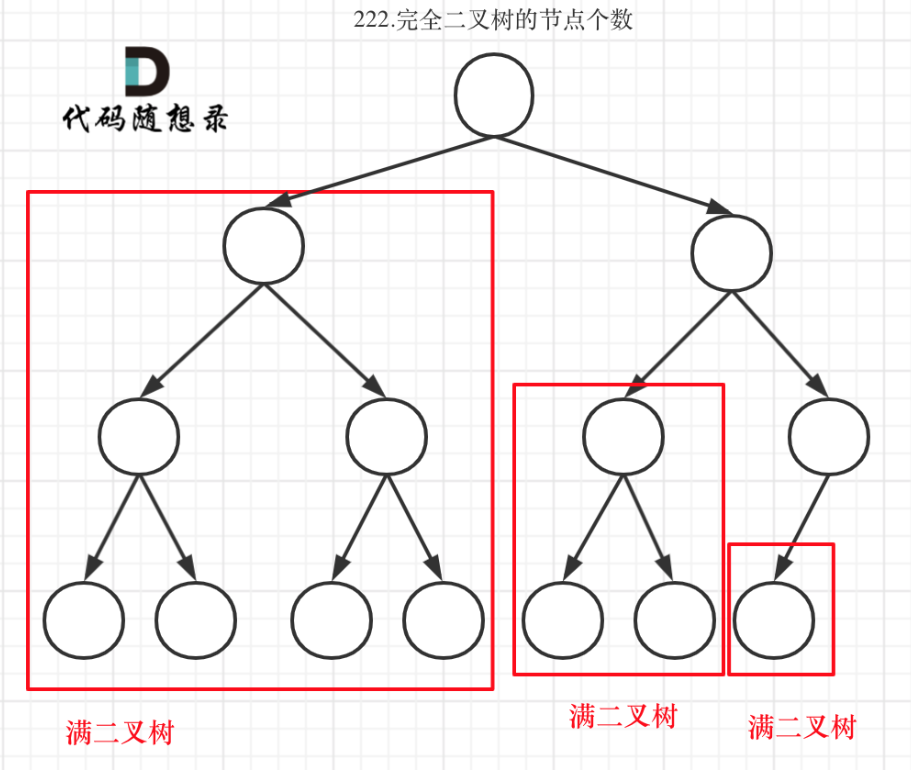对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。 *
对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算
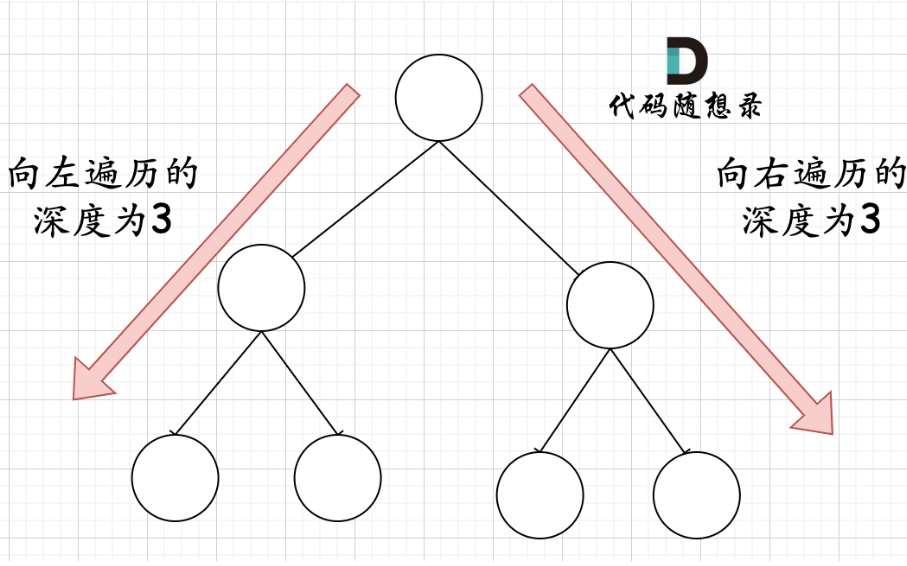可以达到